LED摩托车信号灯配光设计 (1)

       本文提出了一种基于曲面L ED 阵列的光强分布数学模型的新型方法，在推导了曲面L ED 阵列光强分布数学模型的基础上，将其应用于L ED 摩托车信号灯配光设计。如果能够从理论上建立L ED 光强分布的数学模型，研究一种L ED 阵列的光强分布且无需聚光器和配光镜，使其满足国家标准，从而为L ED 摩托车信号灯设计提供一种新的快捷、实用的方法，具有重要的理论与实际指导意义。　　
　　1 　曲面LED 阵列的光强分布的数学模型
　　1. 1 　单个LED 光强分布的数学模型
　　首先建立单个L ED 光强的分布模型，如图1 所示。其中，探测球面中心为(0 ，0 ，0) ，半径为r ，α表示L ED 光源的水平方向角;β表示L ED 光源的垂直方向角;θ表示单个L ED 光线OM 与光轴OL 的夹角;φ表示L ED 光轴OL 与其在x y 平面投影的夹角;γ表示L ED 光轴OL 在x y 平面投影与Y 轴的夹角。

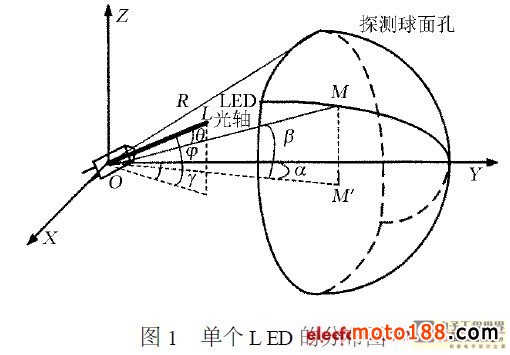
则L ED 光轴对应的单位坐标为(co sφsinγ，cosφsinγ，sinφ) ，探测球面上M点的坐标( rcosβsinα，rcosβcosα， rsinβ) 。
　　由此，L ED 光源的光强分布可以表示为I =I (θ) 或者I = I (α，β) 。
　　而单个L ED 的光强分布不是理想的朗伯体，该分布可以表述为：
　　

 

 
　　当θ =θ1/ 2 时
　　

 

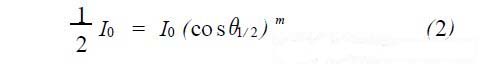
　　即
　　
                  alt="1.LED摩托车信号灯配光设计" src="/uploadfile/mndz/uploadfile/201207/20120716040856461.jpg" width=400>
 
　　     由图1 可知，θ也可以表示为L ED 光轴对应的向量OL 与向量OM 的夹角，则

 

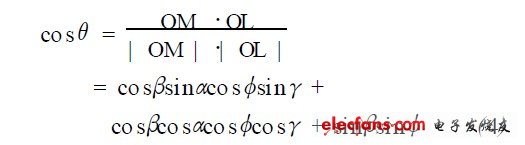
　则

　　
 

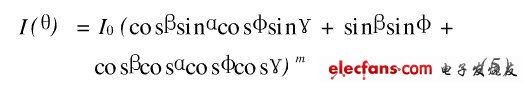
由公式(5) 可知，单个L ED 的光强分布与L ED在空间的倾斜角的垂直分量角φ和水平分量角γ有关，改变φ和γ就可以改变单个L ED 光强的分布。

但是，由于单灯光强小，达不到摩托车信号灯的光强的国标要求，往往需要多个L ED 组合，而改变单个L ED 的倾斜角可以改变光强分布，因此可以进一步研究一种L ED 的曲面阵列排布的光强分布，进而用它来完成对L ED 摩托车信号灯的配光设计。